Abstract
In this paper we present the results of an analysis of the structuring of four-team-per-contest, Swiss (power paired) / elimination tournaments. We create models for teams and tournaments using Python. Team scores are sampled from normal distributions. We estimate the mean and variance parameters of the distributions based on a statistical analysis of the tab of the Chennai World Universities Debating Championships 2014. We provide a discussion of the appropriate methodology for selecting evaluation measurements. We then provide an overview of the more common measures of rank correlation, and rank disorder. We run one thousand iterations of the model of each tournament structure. For each model, the iterations are performed once under the assumption of no team variance, and once using samples from the distributions. The results provide accurate estimates for the population means of the chosen metrics. The no variance iterations isolate the inherent fairness, and suggest the inherent competitiveness, of the tournament structures. The iterations with estimated parameters suggest how fairly the tournament will perform in real world applications. By comparing the performance of the tournament structures, we suggest answers to the following questions: Which bubbling procedure is most fair? Which intra-bracket match-up procedure is most fair? How many rounds should a tournament have? How many randomised rounds should a tournament have? How influential are these decisions on the competitiveness and fairness of a tournament? How fair and competitive are power paired tournaments?
Introduction
The Swiss tournament system was first used in a chess tournament in Zurich, in 1895. Since then, FIDE(the World Chess Federation) has officially recognised five different Swiss tournament structures.1 Originally,preference was given to ensuring board fairness (the equivalent of ensuring that debating teams speak in each position a similar number of times). Over time, more emphasis started being placed on ensuring competitor fairness.
The Swiss tournament structure has a number of attributes that make it an incredibly desirable format for debating tournaments. It can be completed in significantly fewer rounds than a Round Robin. Round robin tournaments also pair up the weakest teams against the strongest, which can be undesirable. In comparison to elimination tournaments, the Swiss system has the advantage of allowing everyone to compete in all of the (prelim) rounds.
However, in porting the Swiss system to British Parliamentary debating, new problems have been introduced. The fact that ordering problems exist is common knowledge. We do not, however, know the severity of the problem; and the precise nature of its causes is often confused.
In this paper we will be looking at the prelim stages of a Swiss/elimination tournament. The fact that there is an elimination phase after the prelims, is important in so far as it requires us to look at the ’break’ ordering of the prelims. We will not, however, be looking at the elimination stage per se. We begin by investigating some of the more relevant differences between chess and debating, and the problems which they cause.
Causes of Power Pairing Failure
The Monotonicity Problem
One of the FIDE rules, which apply to every tournament structure, is that no two players may face each other twice. The primary reason for this is rather simple: if teams repeatedly face each other, then they will be taking too many points off each other. The result is that lower ranked teams can easily ’catch up’, and,therefore, the difference between teams on the tab will no longer have any relation to the true difference in skill between the teams. In effect, the tab is ”compressed”.2 Again, it is well known that the middle of the tab often ’catches’ the top rooms, when teams in the top rooms are constantly taking points off each other. This may appear to make the tournament more exciting, but it is not too difficult to imagine the injustice that may result. Consider a team just below the break who repeatedly catches a team just above it. The higher rated team may win several of these encounters. However, the lower rated team only needs to win once(at the end), in order to break, above the better team. This is the case no matter how much better the higher rated team actually was. By forcing monotonicity, chess tournaments allow the gap between teams to widen, until they reflect the true difference in ability between the teams.
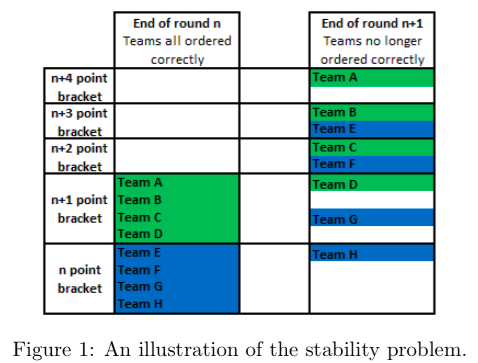
The Stability Problem
Arguably the most serious concern with power pairing, is its instability. This refers to the fact that the tab doesn’t converge to any particular order. After settling, it fluctuates, quite significantly, around the correct order. This is true even in the complete absence of any upsets. The source of this problem lies in the fact that four teams compete in each BP debate. By awarding more than one point for a win, power pairing enables teams to ’jump’ over brackets, without having had to face any team in that bracket. By ’bracket’,we mean a group of teams in a tournament that are on the same number of points (the WUDC Constitution uses the word ’pool’ to mean the same thing). For example, should one bracket have 4 teams on n points,and another bracket have 4 teams on n+1 points, 2 of the teams on n points will end up above a team who started on n+1 points. Necessarily.
In the initial stages of the tournament, this is not much of a problem. However, once a portion of the tab has settled, then running another round will disorder that portion. Since different parts of the tab settle at different times, a significant portion of the tab is always going to be getting more disordered each round. The result, is an upper limit to how ordered the tab can get, before the order starts fluctuating, and the degree of order levels off towards an asymptote. This does, of course, only happen when teams are close together. The monotonicity problem described above ensures this compression. In that sense, these two problems are mutually re-enforcing
Creating A Metric for The Disorder of Tabs
There is a considerable amount of literature on the subject of disorder, and several definitions from which we can choose. As Paul Collier notes,3 one should always try and use criteria set by other researchers, so as to avoid the temptation to define your hypothesis to be correct. None the less, many measures of disorder are inappropriate for tournaments.4 We therefore offer a brief discussion of how we selected our criteria
Interpretability
In this paper, we are primarily interested in practically significant differences. To that end, we would like our metrics to be interpretable. That is to say that they should have an obvious meaning. Measures such as the Kendall τ coefficient and Goodman and Kruskal’s gamma, are popular, and well suited to hypothesis testing. However, they don’t offer any insight into the absolute disorder of a list.
Robustness
In tournament evaluation, we must fully account for outliers. If a team is severely disadvantaged by a tournament, it will be no consolation to the team that this was a rare event. Tournament structures need to be designed to ensure that every instantiation meets some minimum criteria of fairness (in the absence of variance attributable to the teams). Therefore, we use some statistics which are noticeably volatile.
Consideration for The Break
It is again well known that power pairing has a preference for the extremes. That is to say that the top and bottom few teams in each tournament will be relatively better ordered than the middle. An important part of the preliminary stages of a tournament is the ranking of the break teams. This is unique to our purposes,and traditional measures of disorder will not take this into account
Metrics Used
Preliminary Definitions:
•A team’s “rating” is where they should have placed in the tournament
•A team’s “ranking” is where they actually placed
• “The break” refers to the top ranked 16 teams
Measurements on The Entire Tab
Spearman’s Footrule Distance: Spearman’s Footrule Distance is the sum of the differences between the ratings and the rankings of the teams5
Spearman’s ρ Distance: The Spearman’s ρ distance is similar to Spearman’s footrule, however, it exaggerates outliers, by squaring the distances before summation6.
Measurements on The Break
Measurements Relating to The Correctness of The Break
Break upsets: Break upsets is the number of teams that should have broke, but didn’t. Equivalently, it is the number of teams that shouldn’t have broke, but did.
Break-loser: The break loser is the top rated team to not break in a tournament. Ideally this is the team rated 17th. If the number is significantly lower than this, then it will indicate that a strong team has been severely disadvantage in that tournament
Measurements Relating to The Ordering of The Break
Spearman’s Footrule Distance on The Break: We re-rate the teams who have made the break from 1 to 16. The Spearman’s Footrule Distance is then calculated as normal.
The Models
How the Models Calculate Intra-Bracket Match-ups and Bubbles
Bubbling
Bubbling is the procedure whereby the tabbers adjust the brackets in order to make each bracket consist of a number of teams that is divisible by four. The WUDC Constitution, Art 30(3)(c), states that “If any pool (The Upper Pool) consists of an amount of teams equivalent to a number that is not divisible by four,then teams from the pool ranking immediately below that pool (The Lower Pool) may be promoted to the Upper Pool…” This is a somewhat cumbersome provision.7. However, it is clear that bubbling must consist of ’pull ups’. We investigated three different ways of selecting the teams from the lower bracket that need to be bubbled up:
• Low: Teams in the lower bracket will be bubbled starting from the bottom, in terms of rating. See Figure 2.
• High: Teams in the lower bracket will be bubbled starting from the top, in terms of rating
• Random: Teams in the lower bracket will be bubbled randomly. Note that this is currently what the WUDC Constitution requires
The WUDC Constitution, Art 30(3)(d) provides that “Once the pools have been adjusted in accordance with 3(c) then the pools are divided into debates of four teams”. We investigated three different ways in which this can be done:
• Splitting: Teams in a bracket will be paired in the same way as teams 17th to 48th in Art 30(5)(b)of the WUDC Constitution, adjusting for bracket size. See Figure 3.
• High-High: The top four rated teams in bracket will form a room, continuing as such through thebracket
• Random: Teams in a bracket will be paired randomly. Note that this is currently what the WUDC Constitution requires.
The Model Without Upsets
We rate 3668 teams from 1 to 366. The top rated team in every room will always win, followed by the next highest rated team, and so on. The only differences in outcome, over the various iterations of the model, are due to the first round, which is completely randomised, as in Art 30(2)(g) of the WUDC Constitution.
Model With Upsets
An upset is any debate result in which a team places higher than a team which was ”better” than them. This happens when variance is introduced to the team’s performances. We wish to investigate how well the different tournament structures tolerate variance. I.e. are the results still reasonably accurate, when a couple of upsets occur? It must be stressed, however, that too much weight should not be afforded to these results. Teams have been modelled based on the 2014 Worlds tab, with the average speaks of each team in each round being used to estimate the mean and variance of each team’s speaks.9 From these populations, the model will sample scores for those teams in each round. Unlike in the case of no upsets, we now have to determine what the ratings of the teams ”should” b. This question is not a trivial one. The first question is whether the estimated population means, or the actually attained means, should be used for comparison purposes. We decided that the latter would be more appropriate. An iteration of the model which samples,on average, higher or lower than the population mean, models a case where a team performs better or worse at that given tournament than they would normally be expected. It is only right that they should thus place higher or lower, respectively. The second question is more tricky. It concerns whether a team with a lower mean score than another team might actually be “better” in some sense than that team. The best estimate,of course, is that they are not. However, see section 7.5 for a discussion of this problem.
Results
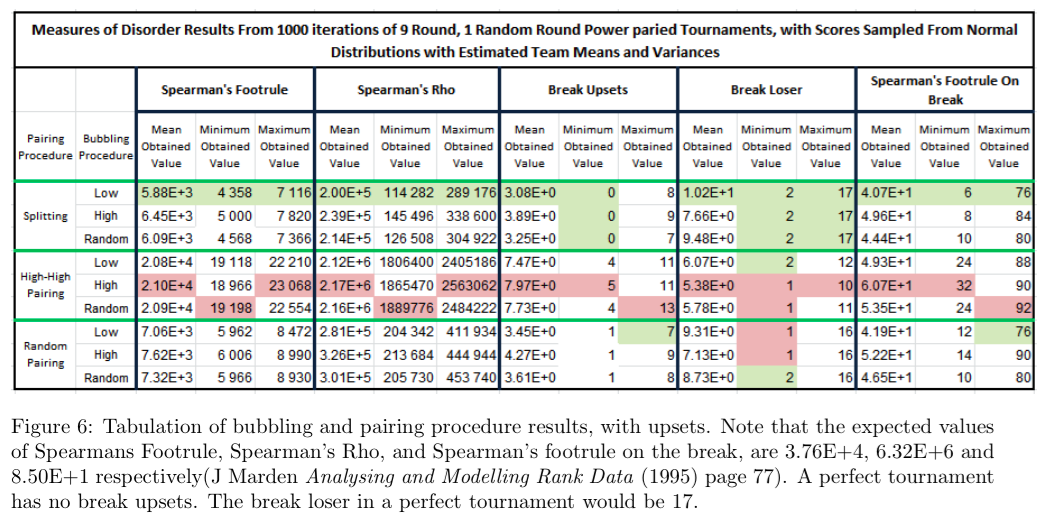
Figure 4 and 6 tabulate the results of the different bubbling and pairing10 procedures, for a 9 round tournament with 1 random round. Figure 4 shows results without upsets, figure 6 shows results with upsets. Figures 5 and 7 are plots the five number summaries of the Spearman’s Footrule distance results from tables 4 and 6. “High-High” pairing permutations are on a separate axis, because the values of their five point summaries are all orders of magnitude above those from the summaries from the other permutations. Figure 8 shows how the mean of the Spearman’s Footrule distance decreases as the number of rounds in a tournament increases. The tournament structure used is one with random pairing and bubbling. Note how the graphs level off towards an asymptote. Figure 9 shows the effect on the mean of the Spearman’s Footrule distance, when more rounds in the tournament are allocated to completely randomised pairing (as in Art30(2)(g) of the WUDC Constitution). The total number of rounds remains constant, at 9. The tournament structure used is one with random pairing and bubbling.
Interpreting the Results
A Note on Speaker Scores
Any non-randomised tournament structure will necessarily need to compare teams who are on the same number of points. The most obvious way to do this is by using team average speaker scores. It might therefore be worth discussing some issues raised in English and Kilcup’s Article, Abolish Speaker Tabs.11 First, it must be noted that the team’s average speaker score does not suffer from all of the problems of individual speaker scores, described in English and Kilcup’s article. Second, if speaker scores are used in determining match-ups or bubbling, I would recommend not using the total speaks up to that round (which is what our model used). Rather, use the speaks from only the previous round. This will both make each round more competitive, and will ensure that outlier speaker scores only affect a team once. Third, it must be noted that there are many alternatives to speaker scores, which can also separate tied teams. Chess systems have had to develop measures of relative strength based only on wins, because you don’t get a score in chess, you only win or lose. For example: the Buchholz System takes the sum of the points of each of the opponents faced by a team. “Direct Encounters”, splits players (teams) based on who performed best when they faced each other. “Number of games played as black”, is self-descriptive, and is used because black is considered more difficult. This could find an analogue as ”number of debates as Opening Government”, or whichever position has been weakest. There are several other systems as well,1 and new ones could be created for debating (such as WUDC Constitution Art 4(a)(iii)).
Fairness and Competitiveness
Fairness is what we have been directly measuring with the model. It concerns whether the better teams in a tournament do actually do better, and if not, how evenly teams are prejudiced. A related, but not equivalent concept is that of competitiveness. Competitiveness refers to the extent to which a tournament incentivises teams to perform at their best. In any tournament where future round match-ups can be both predicted by the teams, and affected by them, there may arise an incentive to perform poorly. In theory, a tournament that is fair will not be uncompetitive. In practice, unfair tournaments can be competitive, and vice versa. For example, elimination tournaments are very unfair, have predictable future rounds, and yet are very competitive. This is because teams can’t affect who they face in future. They either face whoever gets assigned to them, or they drop out. By contrast, round robins are the most fair tournament structures,and yet they often become highly uncompetitive. This is because teams who do badly early on start taking the tournament less seriously. It is apposite to mention here the analogous effect of dropping blind rounds. When teams reach a point where they either have enough, or too few points to break, it will affect their performance, if they are aware of the fact.
How Do the Tournament Structures Support Competitiveness?
Broadly speaking, randomisation supports competitiveness through unpredictability. Splitting brackets, and bubbling low, support competitiveness by creating incentives to score high. Pairing high, and bubbling high, do not support competitiveness at all, because they create incentives to score low. Note that these considerations only apply to speaker scores, not points.
How Do the Tournament Structures Support Fairness?
We submit that the only way for a tournament to be more fair, is to order the teams better, and minimize outlier teams. It could be argued that a tournament which does a worse job of ordering teams, is in fact more ”fair”, if it prejudices teams on a random basis. This is fallacious reasoning. If a team ends up being severely disadvantaged, due to a combination of randomly being bubbled up more often than other teams and/or randomly drawing the strongest teams in the bracket more often than other teams, it will not be any consolation that this was a rare event, nor will it help that all the other teams in the tournament had stood an equal chance of being so disadvantaged.13 That random can be unfair, is perhaps even more evident when considering completely randomised rounds, in figure 9. More completely randomised rounds aren’t even less fair by the Spearman’s Footrule metric, they are more fair, and yet one would undoubtedly still be very cautious of having too many completely randomised rounds. The reason is simple, some teams might be disadvantaged too much in having to face very strong teams. These same sorts of black swan events can happen within brackets. Evidence of this can be found by looking at the maximum values of the metrics in figures 4 and 6. In particular, the Spearman’s Rho metric, which exaggerates outlying teams within a tournament. Notice how the Spearman’s Rho maximum for ”Random Random” is more than double that for ”Splitting Low”, in the no upsets table. If one can appreciate that completely randomised rounds may be unfair, then it should not be too much of a stretch to imagine that randomised pairing and bubbling, which do worse than other tournament structures, by the Spearman’s Footrule metric, may be unfair as well.
Understanding Bubbling and Intra Bracket Pair-Ups
Pairing teams high-high, and bubbling high teams, was historically a popular method. The argument for this system is probably based on the mistaken assumption that, because power pairing pairs off teams on the same or similar points, it should pair off teams on the same or similar speaks. Two differences between speaks and points make this reasoning erroneous. Firstly, the tab doesn’t weight speaks equally to points. Ranking is by points first, and then by speaks. The primary objective of any debating tournament is there-fore to ensure that teams get the correct points, not the correct speaks. By bubbling and pairing high,it is the teams in the bracket that should have got the most points from a round, who are now the most disadvantaged.14 The second difference, is that points are zero sum. This means that, ceteris paribus, the other teams in your room will determine how many points you get. Speaks, however, are largely (though admittedly not entirely) independent of the other teams in the room. Therefore, if the tournament is also interested in getting a good speaks ranking, it doesn’t matter much where teams are.
There is also an interaction between bubbling, and the stability problem described in section 2.2 above. Recall that some of the teams in a bracket will end up outranking teams in the bracket above them, when each new round is run. Bubbling high means that it won’t even be the best teams in the lower bracket who “jump” in this way. It will be the teams below the best teams; the best teams having just bubbled up.
Low bubbling is perhaps counter intuitive. The logic behind it is that the teams in the bracket who were originally expected to lose, should be the ones who are disadvantaged. Bubbling is always going to be a problem for someone. With low bubbling, in the absence of upsets, things will go almost the same way they would have, if no bubbling had taken place (but see section 7.5). Perhaps most importantly, low bubbling increases the stability of the tournament. When the top teams in a bracket ”jump” over the teams in a higher bracket, some of those teams that they jump over will now be teams that had bubbled. I.e. teams that they would normally beat anyway.
Splitting brackets is analogous to low bubbling. It affords the teams who are better on average the greatest chance of winning.
Last Note on Variance and Upsets
One could always simply rank teams by their total speaks. If speaker scores were completely reliable, then this tournament would, by one rating method, be perfectly fair. However, even assuming that speaker scores are completely reliable, there are reasons why such a tournament would not be preferable. Tournaments should give teams a chance to recover from bad rounds, to do well when it counts, etc. In this way, a team may rightly be considered ”better” than a team that outscores them. Similar reasoning reveals a problem with low bubbling. At a given stage in a tournament, the best estimate is always that the bottom teams in a bracket ”should” generally lose the next round (if there are no upsets). Yet no-one would suggest giving these teams an automatic fourth. The purpose of having a full tournament in the first place, is to give them a chance to do better. By extension, it cannot be correct to make it unreasonably difficult for them to do well. Some amount of outright upsets in a tournament may even be considered healthy. The same problem also presents itself when splitting brackets. However, it does so to a much smaller extent. We maintain that a tournament should, at a minimum, seek to be fair in the absence of any upsets. However, the importance of variance in speaker performance must not be overlooked.
Conclusion
It is apparent that the preliminary rounds of debating tournaments cannot be considered to be particularly fair. The two largest reasons for this problem, are probably the lack of monotonicity, and the stability problem, caused by art Art30(3)(h)(ii) and (iii) of the WUDC Constitution. As a result, we suggest the following:
• The prelim rounds should only be seen to ensure that at least a large portion of the top 16 teams in a tournament will continue to the break rounds. The tab should not be considered to have any further value.
• As a direct consequence of the above, all Swiss tournaments must have break rounds. Tournaments structures such as that used at the South African WUPID qualifier, 2014, which consist of only power paired rounds, must not be used again. If it is desired that every team is able to speak in every round, then a round robin format must be followed.
• Tournament organisers, and the WUDC, should seriously investigate the possibility of placing at least some upper bound on the number of times that teams may see each other
• It has been shown that splitting brackets for match-ups, and bubbling low teams, significantly reduces the unfairness of tournaments. However, the bubbling structure is much less influential, and low bubbling presents its own concerns, which might outweigh its benefits. Splitting brackets, however,should be seriously considered as an alternative to randomisation.
•No tournament should ever match up teams high-high, or bubble up high teams.
http://www.fide.com/component/handbook
The other reason is obvious, tournaments are also just more fun when teams get to see a larger number of different teams.
Collier, P The Bottom Billion (2007) page 18
For example, many of the measures of the disorder of a list, are tailored to measuring the number of CPU cycles required for a computer to sort the list.
Diaconis, P & Graham, R. L Spearman’s Footrule as a Measure of Disarray Journal of the Royal Statistical Society. Series B (1977) Vol.39(2) page 262-268
Diaconis, P Spearman’s Footrule as a Measure of Disarray
Why not just: ”…consists of a number of teams that is not divisible by four…”?
There were 340 team at Worlds 2014. We drop four, because not all teams completed in all the rounds.
We recognise that speaker scores are somewhat unreliable. However, they are certainly the best estimate available for the absolute strength of teams, for the purposes of modelling upsets. See also section 7.1, for more on this.
The word pairing doesn’t accurately capture the fact that there are four teams in a debate. But we use it for convenience.
M English & J Kilcup Abolish Speaker Tabs Monash Debate Review (2013)
http://www.fide.com/component/handbook
The FIDE chess rules, in addition to monotonicity, require that a team may only bubble once per tournament.
It also has the effect of inflating the scores of the teams who don’t bubble. However, low bubbling also has the effect of deflating the remaining team’s scores. Thus, between low and high bubbling, this a moot point.